-
论文名称:VoxelNet: End-to-End Learning for Point Cloud Based 3D Object Detection
-
论文作者:Yin Zhou, Oncel Tuzel (Appple Inc)
-
收录情况:CVPR 2018
简介
VoxelNet,是较早探索体素化处理点云的方法,初衷是设计端到端神经网络,减少使用手工设计的点云特征;作者受2D目标检测中成熟的$region~proposal~network~(RPN)$启发,将它推广到3D检测框预测,问题是RPN需要张量形式的稠密数据输入,这与点云稀疏、不规则的特点不符,为此作者引入了Voxel Feature Encoding Layer, 将原始点云逐步处理,提取特征,形成高维张量数据。 实验部分作者设计了baseline检测方法,使用人工定义的特征,和VoxelNet对比,在KITTI数据集汽车类物体上优于其他方法。现在来看思路比较清楚,结果相对可靠, 在雷达点云—3D目标检测领域产生了较大影响力。
主要方法
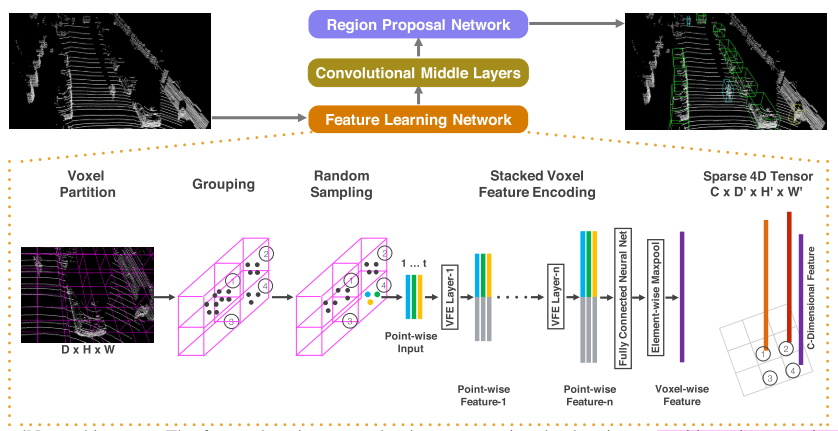
- VoxelNet 架构如上图所示,由三个模块组成:
- Feature learning network
- Convolutional middle layers
- Region proposal network
- Feature learning network
- 体素划分。点云大小为$D, H, W$,每个体素的尺寸 $v_D, v_H, v_W$,所以体素网格的个数 $D’ = D/v_D, H’ = H/v_H, W’ = W/v_W$
- 点分组。每个体素内部的点是一组,每组包含的点数不一定相同
- 随机采样。在每组内部随机采样,采样点数固定为$T$,目的是减少运算量
- 提取体素内点云特征。这篇文章提出了 Voxel Feature Encoding Layer (VFE Layer),如下图,堆叠多个VFE Layer输出提取的特征
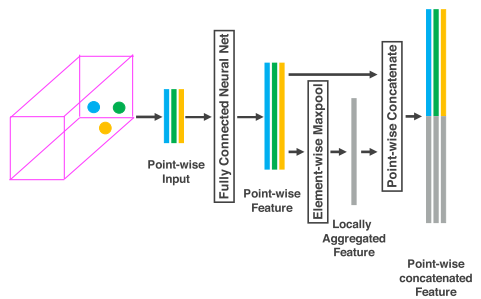
- 用$\textbf{V}$表示一个体素,\(\textbf{V} = \{\textbf{p}_i = [x_i,y_i,z_i,r_i]^T \in \mathbb{R}^4\}_{i=1 \dots t}\)
- $r_i$ 是反射率
- $(v_x, v_y, v_z)$ 是 $\textbf{V}$的中心,就是所有点坐标的平均值
- 对 $\textbf{p}_i$ 进行变换,得到 $\hat{\textbf{p}}_i$
- \[\textbf{V}_{in} = \{ \hat{\textbf{p}}_i = [x_i,y_i,z_i,r_i,x_i-v_x,y_i-v_y,z_i-v_z]^T \in \mathbb{R}^7\}_{i=1 \dots t}\]
- 和中心点做差,相当于编码了点云表面形状信息
- 再用全连接网络对 $\hat{\textbf{p}}_i$ 作变换,得到新的特征 $\textbf{f}_i \in \mathbb{R}^m$
- 全连接网络很常见:线性层、BN层、ReLU层
-
再对所有的 $\textbf{f}_i$ 做对应维度的最大池化操作,得到体素$\textbf{V}$整体的特征 $\tilde{\textbf{f}} \in \mathbb{R}^m$
-
然后连接 $\textbf{f}_i$ 和 $\tilde{\textbf{f}}_i$,得到 $\textbf{f}_i^{out} = [\textbf{f}_i^T, \tilde{\textbf{f}}] \in \mathbb{R}^{2m}$
-
所以体素$\textbf{V}$提取特征后的输出为 $\textbf{V}_{out} = {\textbf{f}i^{out}}{1 \dots t}$
- 堆叠 $n$ 次,,最后一个VFE Layer输出 $C$ 维的体素级的特征表示
- 稀疏的张量表示。整个点云表示成了 $C \times D’\times H’ \times W’$ 维度的张量
- 超过 90% 的体素是空的,这是加速的关键
- 剩余非空体素表示成了这样的张量
- Convolutional middle layers
- Conv$M$D($c_{in}, c_{out}, \textbf{k},\textbf{s},\textbf{p}$) 表示$M$维的卷积操作,前2个参数是输入输出维度,后3个是kernel、stride、padding维度
- 如果$\textbf{k}$中3个数值一样,如 $k=(k,k,k)$,就用一个标量$k$表示$\textbf{k}$
- 每个卷积中间层,操作都是3D卷积,BN,ReLU序列化的操作
- 因此,卷积中间层把 voxel-wise features 作了一系列非线性变换,形成更抽象和高层特征
- Conv$M$D($c_{in}, c_{out}, \textbf{k},\textbf{s},\textbf{p}$) 表示$M$维的卷积操作,前2个参数是输入输出维度,后3个是kernel、stride、padding维度
- Region proposal network
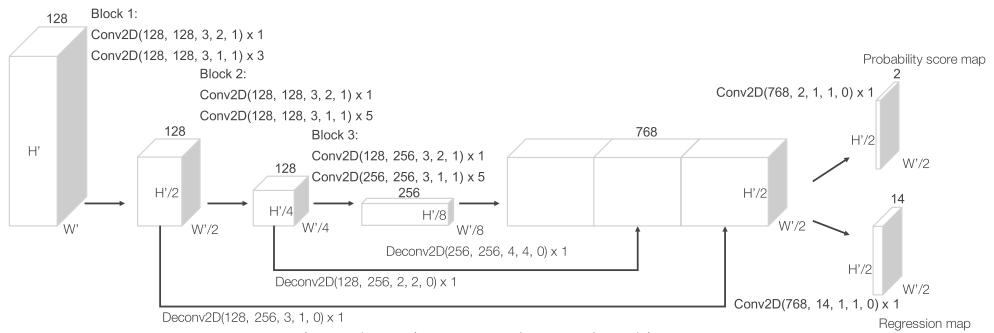
- 这部分是参考Faster RCNN中的RPN,从行文思路来看,借鉴RPN在2D目标检测的成功经验,应用到3D目标检测中
- 输入:卷积中间层的输出
- 输出的probability score map、regression map维度没搞清楚什么含义?
- 损失函数设计
- positive anchor 集合$N_{pos} = {a_i^{pos}}_{i= 1 \dots N_{pos}}$,和ground truth关系是?我觉得是IoU大于阈值的anchor,是positive anchor,也就是预测产生的
- positive anchor 表示为 $(x_c^a, y_c^a, z_c^a, l^a, w^a, h^a, r^a)$
- ground truth 3D box表示为 $\textbf{u}^* = (x_c^g, y_c^g, z_c^g, l^g, w^g, h^g, r^g)$,分别表示中心点、长宽高、偏航角(物体朝向)
-
negative anchor 集合$N_{neg} = {a_i^{neg}}_{i=1 \dots N_{neg}}$
-
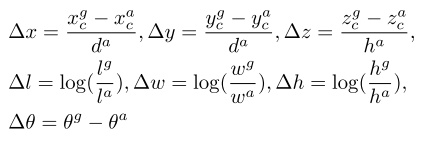
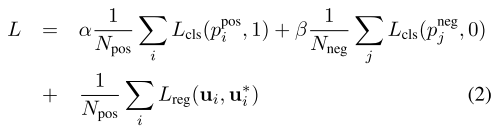
- 二值交叉熵分类、SmoothL1回归
- 上下文有矛盾?
- 这里没搞明白,回归的到底是数值本身,还是数值的偏移量?
- 注意:算回归损失时,只算 positive anchor 的损失
- positive anchor 集合$N_{pos} = {a_i^{pos}}_{i= 1 \dots N_{pos}}$,和ground truth关系是?我觉得是IoU大于阈值的anchor,是positive anchor,也就是预测产生的
实验
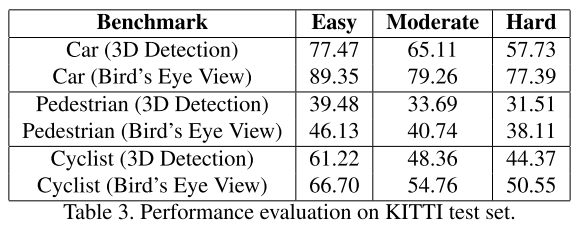
- 数据集:KITTI。测试集结果要提交服务器才能得到,作者主要在验证集实验,测试集展示了自身结果,没有对比
- 训练集/验证集,划分方法值得借鉴
-
验证集,鸟瞰图结果
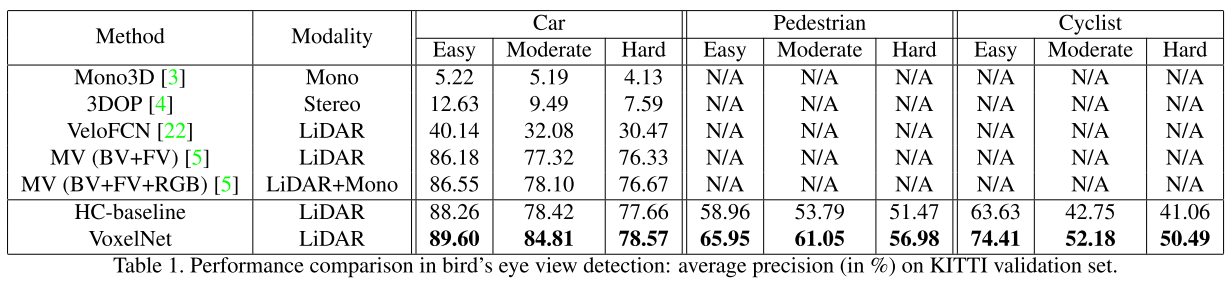
-
验证集,3D检测结果
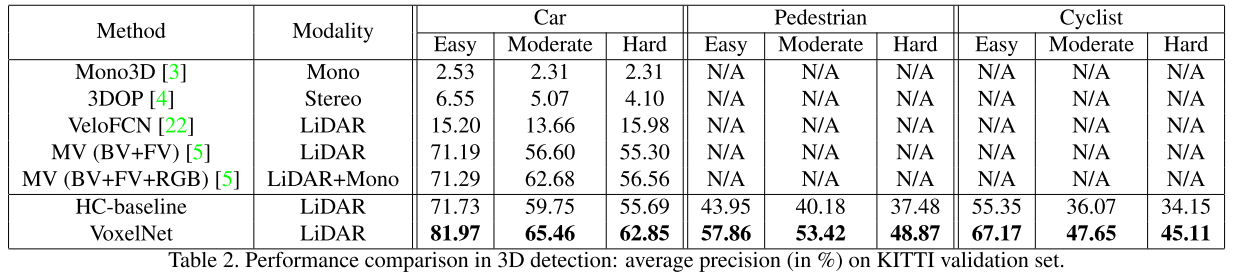
- 测试集,检测结果