这篇论文是在MarrNet基础上的工作,研究内容是物体3D形状重建,重点放在了可扩展性上,即从已知物体学习,结合一些先验知识,重建出训练集没见过的物体的3D形状,创新性比较大。
-
论文作者:Xiuming Zhang, Zhoutong Zhang, Chengkai Zhang, Joshua B. Tenenbaum, William T. Freeman, Jiajun Wu(MIT CSAIL, Google Research)
-
收录情况:NeurIPS 2018
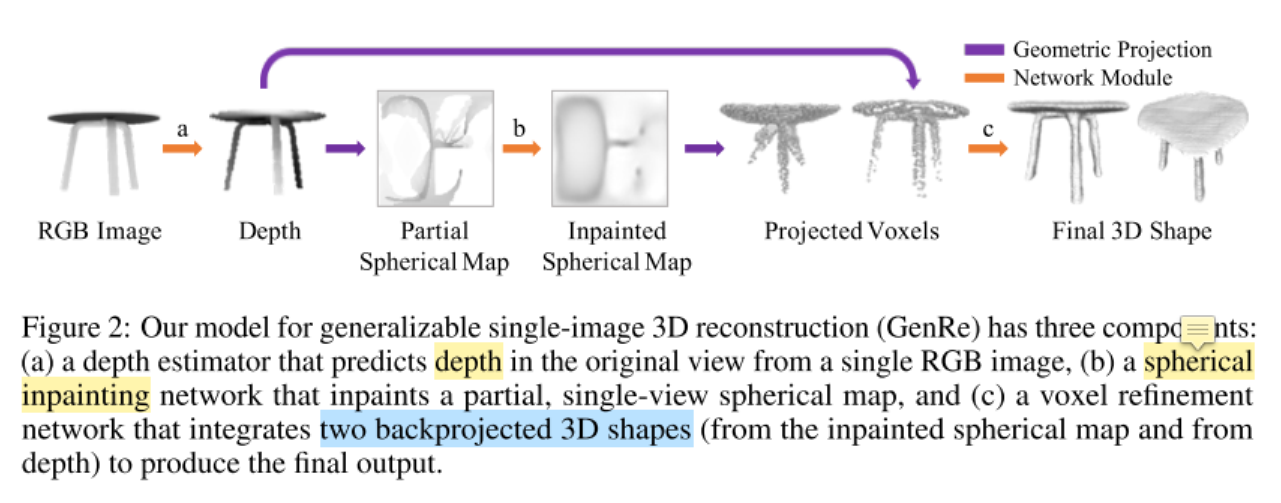
主要方法
利用单张图片的重建算法,学习一个函数 $f_{2D \rightarrow 3D}$,把图片中的2D物体映射成3D形状。本文通过正则化 $f_{2D \rightarrow 3D}$ 解决扩展性的问题。使用的正则化方法是把 $f_{2D \rightarrow 3D}$ 分解成 $geometric~projections$ 和 $learnable~reconstruction$ 模块。
本文的方法——$GenRe$,由3个可学习的模块组成,通过 $geometric~projections$ 模块连接。
-
第一个模块是单视图的 depth estimator $f_{2D \rightarrow 2.5D}$。输入是RGB图,输出是depth map,depth map可以理解成物体的可视化表面(因为获取深度的时候,计算的是相机到物体表面的深度)。因此,给定部分估计的深度图,重建问题变成了预测物体完整的表面。
- 因为物体3D表面很难形式化地表示出来(为什么这么说,因为物体表面不尽相同,不可能用一个方程完全表示,只能是选取一个函数作近似),这里使用球形图作近似(球形图,比较规则图形,方便用方程描述)。
- $geometric~projections$ $p_{2.5D \rightarrow S}$ 把深度图转换成球形图,具体说是 $partial~ spherical~ map$
- 然后把 $partial~ spherical~ map$ 输入到 $spherical~ map$修复网络,预测修复好的球形图($inpainted~spherical ~map$)
- 然后把 $inpainted~spherical ~map$ 投影到 voxel space
- 因为球形图仅有球形的外表面信息,不能处理沿球体半径的自遮挡,本文使用了 voxel refinement module解决这个问题。
- 输入包含2部分
- 一个是来自 $inpainted~spherical ~map$ 的体素图
- 另一个是来自 $depth~map$ 的体素图
- 输出最终的3D shape
- 输入包含2部分
- Single-View Depth Estimator
- 用带有干净背景的图片,预测物体深度。受MarrNet启发,把深度做为中间表示,能从图片蒸馏得到物体重要的几何信息
- 深度估计是类别无关的,不同形状的物体可能有共同的几何结构,比如衣柜和床都有垂直于地面的表面(这都是自成一说,怎么都能找到支持自己观点的例子)
- Spherical Map Inpainting Network
- 利用球面图,本文把3D表面补全问题转化成2D球面图修复问题(其实本文困扰我的点是,spherical map到底在说什么)
- 作者观察到:用来修复球面图训练好的网络,对未知形状类别具有好的扩展性,如下图所示(???从这幅图真的能看出什么吗)
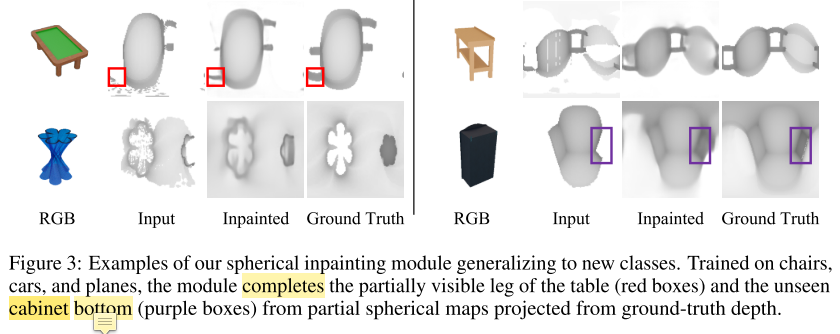
-
与voxel map相比(一般是3D图),因为3D表面的稀疏特性,spherical map处理更高效
- 因为球面图反映了单位球体的信息,设计网络结构时容易想到球卷积。但是本文的 shape reconstruction 不适合球卷积,因为球卷积是在光谱域进行操作。每次往返于频谱域的转换都需要对最大频率进行封顶,从而导致额外的混叠和信息丢失(完全不清楚这段在说什么)。
- 对于识别任务而言,与球卷积提供的卷转不变性的优势相比,信息损失可能能够忽略。但是对于重建任务,信息损失会导致带有低频组件模糊输出。
- 从经验上来看,标准卷积比球卷积更适合重建任务。
- Voxel Refinement Network
- 虽然修复的球形图提供了物体表面在单位球体的投影,但是当自遮挡发生时,表面信息就丢掉了。本文使用精修网络恢复丢失的信息,精修网络在voxel space进行操作,它的输入是两个voxielized shapes:
- 从估计的depth map得到的shape
- 从inpainted spherical map得到的map
-
输出最终重建的形状
- 因为恢复的思路是从遮挡区域的周围得到信息,所以精修网络需要捕获 local shape priors,并且不关心形状类别(class-agnostic)
- 这段是用来支撑上一段的表述:实验显示,当提供ground truth depth map和spherical map时,精修网络在重建训练数据和没有见过的类别形状时,表现都较好
- 虽然修复的球形图提供了物体表面在单位球体的投影,但是当自遮挡发生时,表面信息就丢掉了。本文使用精修网络恢复丢失的信息,精修网络在voxel space进行操作,它的输入是两个voxielized shapes:
实验
- 3D形状表示方法
- voxels:在深度学习时代,体素非常适合表示3D形状,因为它的结构很适合做卷积。本文的模型使用了 $128^3$ 个[0, 1]占用的体素网格(这里[0,1]是个区间,不是0、1两个值)
- DRC、MarrNet 作为比较的方法
- Mesh & point clouds:比体素表示简单一些(???作者的一家之言,其实未必)
- AtlasNet 作为比较的方法(total3dunderstanding 这篇论文也见过这个方法)
- Multi-view maps:多视角深度图
- Daeyun Shin, Charless C Fowlkes, and Derek Hoiem. Pixels, voxels, and views: a study of shape representations for single view 3D object shape prediction. In CVPR, 2018 作为比较方法
- spherical maps:3D 形状能表示成球形图(我理解就是一个球形表面)
- GenRe-1step,从RGB图片直接预测球形图
- GenRe-2step,首先从RGB图片直接预测球形图,再修复球形图
- voxels:在深度学习时代,体素非常适合表示3D形状,因为它的结构很适合做卷积。本文的模型使用了 $128^3$ 个[0, 1]占用的体素网格(这里[0,1]是个区间,不是0、1两个值)
- 数据
- ShapeNet,前人制作的数据集
- 合成的数据集
- 对于每个物体,选取20个视角对应的图,进行渲染
- 在cars/chairs/airplanes这几个类别进行训练,其他类别进行测试
- Pix3D
- 真实图像数据集,包含每个物体的真实形状信息
- 在cars/chairs/airplanes这几个类别进行训练
- 在beds, bookcases, desks, sofas, tables, and wardrobes进行测试
- ShapeNet,前人制作的数据集
- 评价指标:Chamfer distance(CD)
-
\[CD(S_1, S_2) = \frac{1}{|S_1|} \sum_{x \in S_1} min_{y \in S2} \parallel x - y \parallel_2 + \\ \frac{1}{|S_2|} \sum_{y \in S_2} min_{x \in S1} \parallel x - y \parallel_2\]
- $S1$ 和 $S2$ 是一个点集对,取自3D shape surfaces;更准确的说,一个来自最终预测的3D shape,一个来自ground truth 3D shape
-
\[CD(S_1, S_2) = \frac{1}{|S_1|} \sum_{x \in S_1} min_{y \in S2} \parallel x - y \parallel_2 + \\ \frac{1}{|S_2|} \sum_{y \in S_2} min_{x \in S1} \parallel x - y \parallel_2\]
- 一些实验结果
- 由于本文重点是进行可扩展式的3D重建,所以我仅分析这部分结果,对于已知类别的形状,不进行赘述

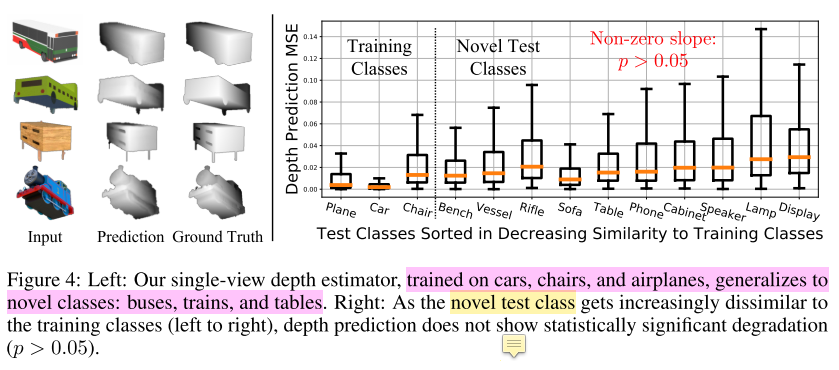
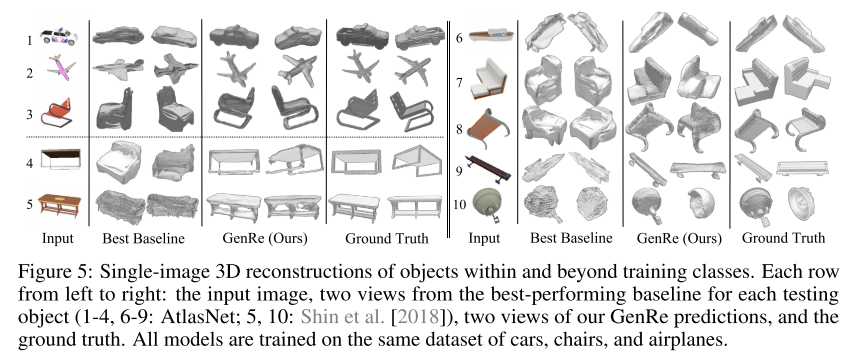

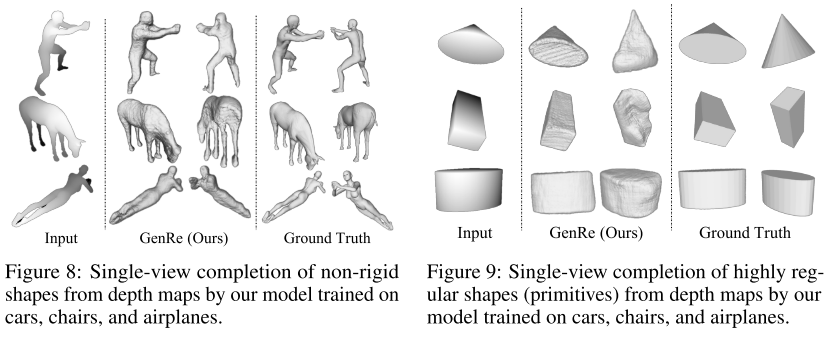
- 由于本文重点是进行可扩展式的3D重建,所以我仅分析这部分结果,对于已知类别的形状,不进行赘述